Appendix A — Common Distributions

A.1 Bernoulli Distribution

Table A.1: Summary of the Bernoulli distribution

Property	Description
Name	Bernoulli distribution
Notation	\(\text{Bernoulli}(\pi)\)
Parameters	\(0 \le \pi \le 1\): probability of success
Support	\(x \in \{0,1\}\)
PMF	\(f(x) = \pi^x (1-\pi)^{1-x}\)
CDF	\(F(x) = 0\) for \(x < 0\); \(1-\pi\) for \(0 \le x < 1\); \(1\) for \(x \ge 1\)
Mean	\(\pi\)
Variance	\(\pi(1-\pi)\)
R functions	`dbern(x, prob)` (PMF) `pbern(q, prob)` (CDF) `qbern(p, prob)` (quantile) `rbern(n, prob)` (random sampling) (from extraDistr* package)*
Special cases	\(\text{Binomial}(n=1, \pi)\) is \(\text{Bernoulli}(\pi)\).

Table A.2: Summary of the Beta distribution

Property	Description
Name	Beta distribution
Notation	\(\text{Beta}(\alpha, \beta)\)
Parameters	\(\alpha > 0\): shape; \(\beta > 0\): shape
Support	\(x \in (0, 1)\)
PDF	\(f(x) = \dfrac{x^{\alpha - 1} (1 - x)^{\beta - 1}}{B(\alpha, \beta)}\)
CDF	\(F(x) = I_x(\alpha, \beta)\), the regularized incomplete beta function
Mean	\(\dfrac{\alpha}{\alpha + \beta}\)
Variance	\(\dfrac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}\)
R functions	`dbeta(x, alpha, beta)` (density) `pbeta(q, alpha, beta)` (CDF) `qbeta(p, alpha, beta)` (quantile) `rbeta(n, alpha, beta)` (random sampling) (base R)
Special cases	\(\text{Beta}(1,1)\) is \(\text{Uniform}(0,1)\).

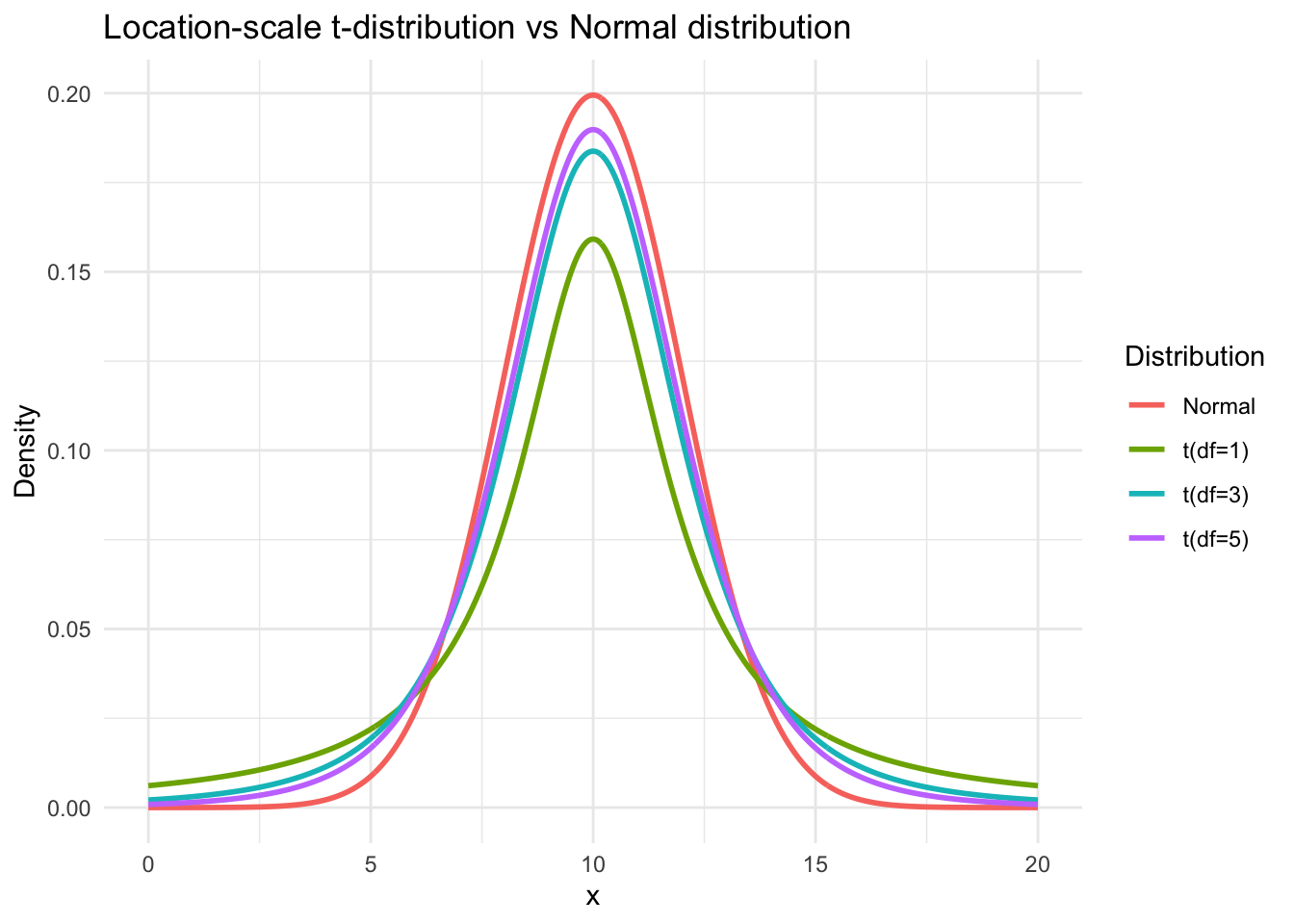
Table A.3: Summary of the location-scale \(t\) distribution

Property	Description
Name	Location-scale \(t\) distribution
Notation	\(t(\mu, \sigma, \nu)\)
Parameters	\(\mu \in \mathbb{R}\): location; \(\sigma > 0\): scale; \(\nu > 0\): degrees of freedom
Support	\(x \in \mathbb{R}\)
PDF	\(f(x) = \dfrac{\Gamma\left(\frac{\nu+1}{2}\right)}{\Gamma\left(\frac{\nu}{2}\right)\sqrt{\nu\pi}\sigma} \left[1 + \dfrac{1}{\nu} \left(\dfrac{x - \mu}{\sigma}\right)^2\right]^{-\frac{\nu+1}{2}}\)
CDF	\(F(x) = T_\nu\left(\dfrac{x - \mu}{\sigma}\right)\), where \(T_\nu\) is the CDF of the standard \(t\) distribution
Mean	\(\mu\) for \(\nu > 1\); undefined for \(\nu \le 1\)
Variance	\(\dfrac{\nu \sigma^2}{\nu - 2}\) for \(\nu > 2\); infinite for \(1 < \nu \le 2\); undefined for \(\nu \le 1\)
R functions	`dt.scaled(x, df, mean = mu, sd = sigma)` (density) `pt.scaled(q, df, mean = mu, sd = sigma)` (CDF) `qt.scaled(p, df, mean = mu, sd = sigma)` (quantile) `rt.scaled(n, df, mean = mu, sd = sigma)` (random sampling) (from metRology* package)*
Special cases	- \(t(0,1,\nu)\): standard Student’s \(t\) - \(\nu \to \infty\): converges to \(\mathcal{N}(\mu, \sigma^2)\) - Heavy-tailed alternative to the normal distribution

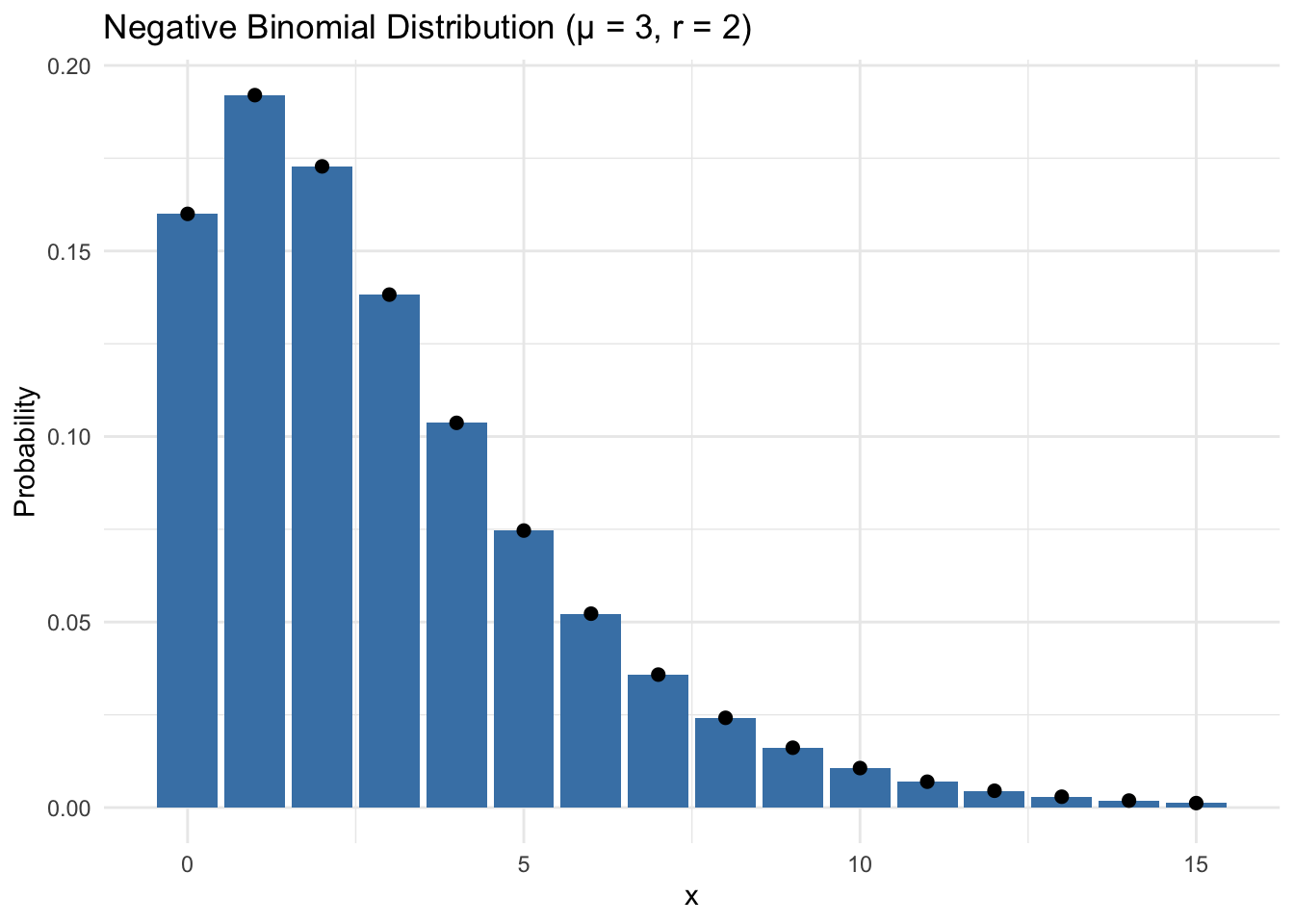
Table A.4: Summary of the negative binomial distribution

Property	Description
Name	Negative binomial distribution
Notation	\(\text{NB}(\mu, r)\)
Parameters	\(\mu > 0\): mean \(r > 0\): size (dispersion)
Support	\(x \in \{0,1,2,\ldots\}\)
PMF	\(f(x) = \dfrac{\Gamma(x+r)}{\Gamma(r)\,x!} \left(\dfrac{r}{r+\mu}\right)^r \left(\dfrac{\mu}{r+\mu}\right)^x\)
CDF	\(F(x) = \displaystyle \sum_{k=0}^{\lfloor x \rfloor} \dfrac{\Gamma(k+r)}{\Gamma(r)\,k!} \left(\dfrac{r}{r+\mu}\right)^r \left(\dfrac{\mu}{r+\mu}\right)^k\)
Mean	\(\mu\)
Variance	\(\mu + \dfrac{\mu^2}{r}\)
R functions	`dnbinom(x, size = r, mu = mu)` (PMF) `pnbinom(q, size = r, mu = mu)` (CDF) `qnbinom(p, size = r, mu = mu)` (quantile) `rnbinom(n, size = r, mu = mu)` (random sampling) (base R)
Special cases	As \(r \to \infty\), \(\text{NB}(\mu, r) \to \text{Poisson}(\mu)\).

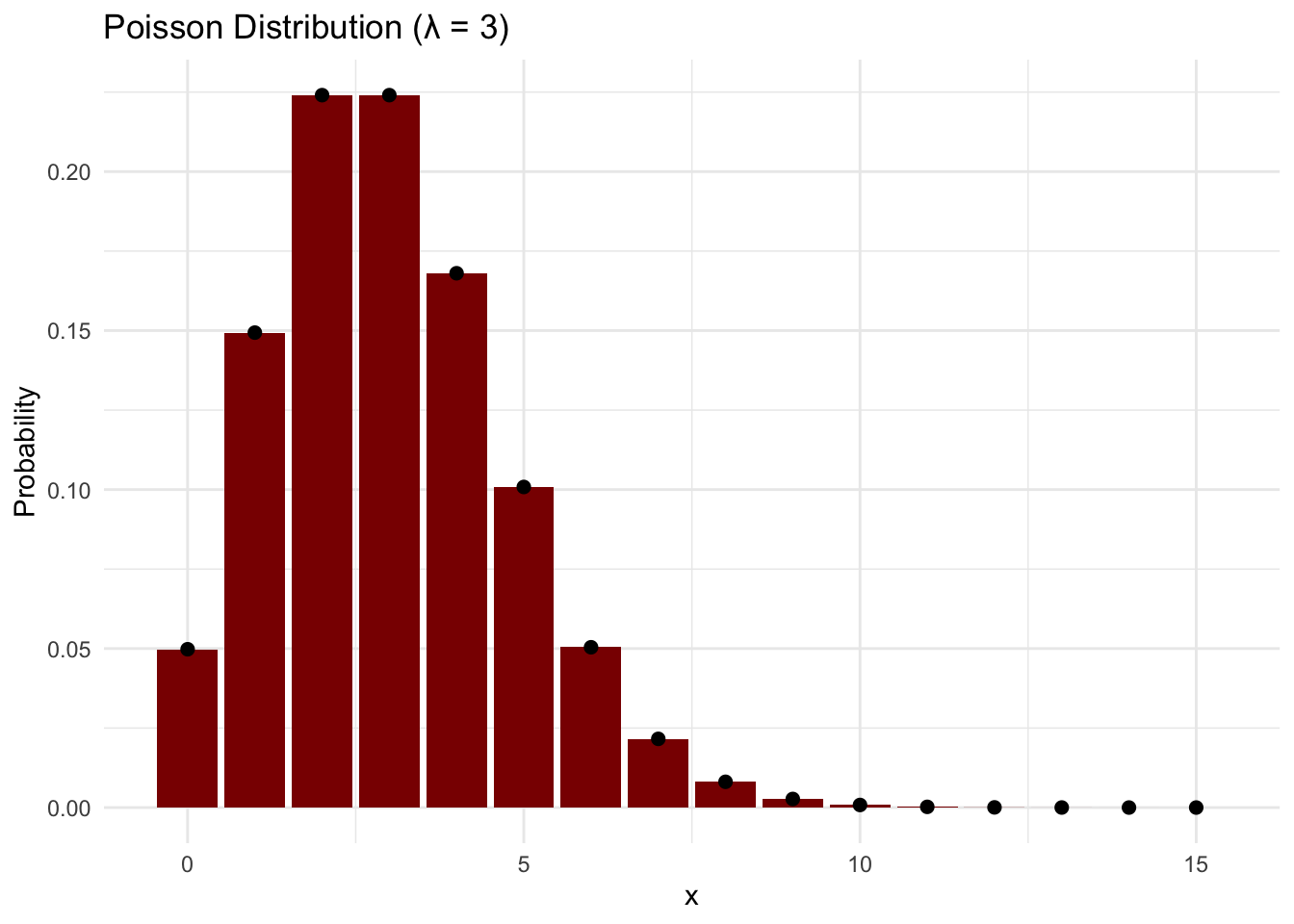
Table A.5: Summary of the Poisson distribution

Property	Description
Name	Poisson distribution
Notation	\(\text{Poisson}(\lambda)\)
Parameters	\(\lambda > 0\): rate (mean number of events per unit interval)
Support	\(x \in \{0,1,2,\ldots\}\)
PMF	\(f(x) = \dfrac{e^{-\lambda} \lambda^x}{x!}\)
CDF	\(F(x) = \displaystyle \sum_{k=0}^{\lfloor x \rfloor} \dfrac{e^{-\lambda}\lambda^k}{k!}\)
Mean	\(\lambda\)
Variance	\(\lambda\)
R functions	`dpois(x, lambda)` (PMF) `ppois(q, lambda)` (CDF) `qpois(p, lambda)` (quantile) `rpois(n, lambda)` (random sampling) (base R)
Special cases	- Limit of \(\text{Binomial}(n,p)\) as \(n \to \infty\), \(p \to 0\) with \(np=\lambda\) fixed - Distribution of counts in a homogeneous Poisson process - Sum of independent \(\text{Poisson}(\lambda_i)\) is \(\text{Poisson}(\sum \lambda_i)\)